vous pouvez retrouver le binaire ici
Ce challenge est une version simplifiée d’un challenge nommé “chaussette”, durant la résolution de sa version compliquée j’ai appris à utiliser miasm, un framework de reverse engineering que j’ai trouvé très intéressant malgré le peu de documentation. J’ai donc décidé de proposer une solution utilisant miasm.
Découverte du challenge
Pour ce challenge, un binaire nous est donné. La commande file permet d’en apprendre un peu plus à son sujet.
╭─user@arch-vmware ~/shared/fcsc2023/reverse/chaussette-xs
╰─➤ file chaussette-xs
chaussette-xs: ELF 64-bit LSB pie executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, BuildID[sha1]=913fe53d14998feda6a550d5a815830cf4ab132f, for GNU/Linux 3.2.0, stripped
On apprend donc que l’on a un ELF x86-64. On va donc l’ouvrir dans ghidra afin d’avoir de comprendre ce qu’il fait plus précisemment.
void FUN_00102140(undefined8 param_1,undefined8 param_2,undefined8 param_3)
{
undefined8 unaff_retaddr;
undefined auStack_8 [8];
__libc_start_main(FUN_00102000,unaff_retaddr,&stack0x00000008,FUN_00103230,FUN_00103290,param_3,
auStack_8);
do {
/* WARNING: Do nothing block with infinite loop */
} while( true );
}
On regard donc le point d’entrée du binaire afin de trouver la fonction main de l’application.
Ici, l’appel à la fonction libc_start_main de la libc nous permet de récuperer notre fonction principale qui sera donc FUN_00102000 .
On va de suite la renommer afin d’y voir plus clair et de la retrouver plus facilement (clic droit sur la fonction -> Rename function).
On arrive donc sur le code principal de notre fonction qui est assez simple à comprendre.
undefined8 main(void)
{
int iVar1;
long lVar2;
undefined8 *puVar3;
ulong *puVar4;
ulong uVar5;
ulong *puVar6;
undefined8 *puVar7;
byte bVar8;
ulong local_18;
undefined8 local_10;
bVar8 = 0;
lVar2 = sysconf(0x1e);
if (lVar2 == 0x1000) {
puVar3 = (undefined8 *)mmap((void *)0x0,0x100000,7,0x22,-1,0);
DAT_001061b0 = puVar3;
*puVar3 = 0x1a22d2ea22d1b848;
*(undefined8 *)((long)puVar3 + 0xf9) = 0xc3f83148b12e2565;
lVar2 = (long)puVar3 - (long)(undefined8 *)((ulong)(puVar3 + 1) & 0xfffffffffffffff8);
puVar7 = (undefined8 *)((long)&DAT_001060a0 - lVar2);
puVar3 = (undefined8 *)((ulong)(puVar3 + 1) & 0xfffffffffffffff8);
for (uVar5 = (ulong)((int)lVar2 + 0x101U >> 3); uVar5 != 0; uVar5 = uVar5 - 1) {
*puVar3 = *puVar7;
puVar7 = puVar7 + (ulong)bVar8 * -2 + 1;
puVar3 = puVar3 + (ulong)bVar8 * -2 + 1;
}
__isoc99_scanf(&DAT_00104004,&local_18);
__isoc99_scanf(&DAT_00104004,&local_10);
lVar2 = (*(code *)DAT_001061b0)(local_18,local_10);
if (lVar2 == 0) {
iVar1 = mprotect(FUN_00103000,0x400,7);
if (iVar1 != -1) {
puVar4 = (ulong *)FUN_00103000;
uVar5 = local_18;
do {
*puVar4 = *puVar4 ^ uVar5;
puVar6 = puVar4 + -0x205ff;
uVar5 = uVar5 * 0x5851f42d4c957f2d + 0x14057b7ef767814f;
puVar4 = puVar4 + 1;
} while (puVar6 < (ulong *)0x1f8);
FUN_00103000(DAT_001061b0,local_18,local_10);
}
}
}
return 0;
}
Il va dans un premier temps allouer 0x100000 octets sur le tas avec les droits de lecture, d’écriture et d’execution grâce à la fonction mmap
Il va ensuite effectuer certaines opérations afin d’écrire des données dans la mémoire allouée, on ne s’attardera pas dessus.
Puis le programme va demander à l’utilisateur 2 entrées. Si l’on regard à l’addresse DAT_00104004 on peut voir qu’elle pointe vers la chaine de caractères : “%lu” ce qui signifie que la fonction scanf va demander à l’utilisateur 2 entiers non signés de 64 bytes.
Enfin, il va appeler le code placé dans la mémoire allouée précedemment avec comme paramètres les 2 valeurs entrées par l’utilisateur.
En fonction du résultat de cette fonction il va continuer l’execution du programme ou non. On comprend donc rapidemment que notre première épreuve va être de trouver les entrées correctes afin que cette fonction retourne 0.
A la suite de cette fonction, si les valeurs entrées sont correctes le binaire va appeler la fonction mprotect() afin d’ajouter les droits d’écriture sur la fonction FUN_00103000 et va ensuite modifier son contenu. Un fois le code de la fonction modifié, il va l’appeler comme argument l’addresse de notre mémoire précedemment allouée ainsi que nos 2 entrées utilisateur.
premier shellcode
La première étape de ce crackme va donc être de trouver les valeurs correcte afin que le code placé en mémoire retourne 0. On va donc utiliser un debugger afin de placer un point d’arrêt au moment de l’appel à la fonction et de récuperer son code.
Pour ma part j’utilise gdb.
Petite astuce d’ailleurs si vous utilisez comme moi ghidra pour décompiler votre code et gdb pour debugger, vous pouvez changer la base address dans ghidra afin que vos addresses soit les mêmes entre ghidra et votre debugger. Il suffit d’aller dans Window -> Memory map ensuite vous cliqué sur la petite maison et changer l’addresse de la base du binaire.
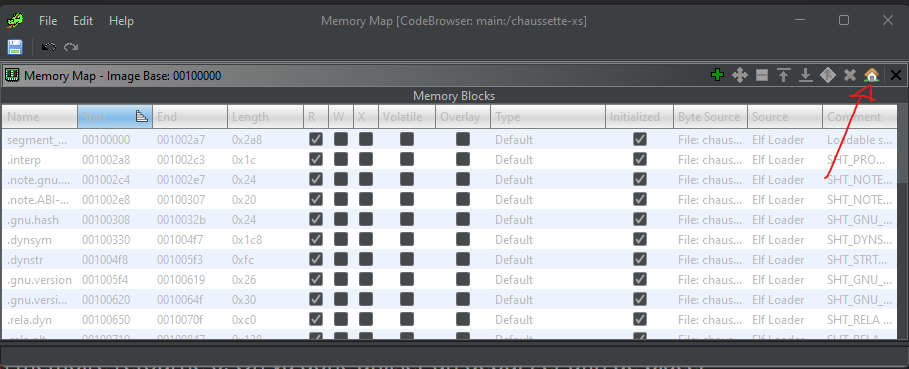
on lance donc gdb, on place notre point d’arret et on lance notre binaire.
(gdb) b*0x5555555560aa
Breakpoint 1 at 0x5555555560aa
(gdb) run
Starting program: /home/user/shared/fcsc2023/reverse/chaussette-xs/chaussette-xs
[Thread debugging using libthread_db enabled]
Using host libthread_db library "/usr/lib/libthread_db.so.1".
123
123
Breakpoint 1, 0x00005555555560aa in ?? ()
(gdb) x/i $rip
=> 0x5555555560aa:
call QWORD PTR [rip+0x4100] # 0x55555555a1b0
On peut voir qu’on est bel et bien arrété avant l’appel à la fonction.
La commande x/i address permet de décoder les opcodes présent à une addresse.
On va donc pouvoir afficher notre shellcode grâce à cette commande.
Attention, ici le code ne se trouve pas à l’addresse mais à l’addresse pointée par celle ci.
(gdb) x/gx 0x55555555a1b0
0x55555555a1b0: 0x00007ffff7cc5000
(gdb) x/100i 0x00007ffff7cc5000
0x7ffff7cc5000: movabs rax,0x33a11a22d2ea22d1
[...]
0x7ffff7cc50ed: mul rdi
0x7ffff7cc50f0: mov rdi,rax
0x7ffff7cc50f3: movabs rax,0xb12e2565d1efe9f8
0x7ffff7cc50fd: xor rax,rdi
0x7ffff7cc5100: ret
On a donc un joli code assembleur, maintenant il faut le résoudre. On remarque d’ailleurs qu’il utilise une seule des entrées utilisateur dans cette fonction. Ce sera de même tout le long du programme, la seconde entrée n’est pas utilisée.
movabs rax,0x33a11a22d2ea22d1
sub rdi,rax
dec rdi
movabs rax,0x94224bcad3296113
or rax,0x1
mul rdi
mov rdi,rax
dec rdi
movabs rax,0xd3b1bf2d4d1d294a
sub rdi,rax
movabs rax,0xbe35746c05e956a9
add rdi,rax
movabs rax,0x5819ea9fcbc8779
xor rdi,rax
dec rdi
movabs rax,0x7f7965e1baca6c8f
sub rdi,rax
neg rdi
ror rdi,0xd
movabs rax,0x4368955c512ca39b
sub rdi,rax
inc rdi
neg rdi
ror rdi,0x32
movabs rax,0x96ccb75bd569807d
sub rdi,rax
inc rdi
movabs rax,0x9f40cb3b786d6842
or rax,0x1
mul rdi
mov rdi,rax
ror rdi,0x14
neg rdi
neg rdi
movabs rax,0x1fd3e4098240e723
add rdi,rax
movabs rax,0xda3d1c27bae9522c
sub rdi,rax
rol rdi,0x36
inc rdi
inc rdi
dec rdi
rol rdi,0x21
rol rdi,0x38
dec rdi
neg rdi
movabs rax,0xc88d84433f7b14e7
or rax,0x1
mul rdi
mov rdi,rax
movabs rax,0xb12e2565d1efe9f8
xor rax,rdi
ret
Il n’est pas très compliqué et aurait pu facilement être résolu à la main, néanmoins pour cette solution on utilisera miasm.
On va dump les octets de ce code dans un fichier, gdb nous permet de le faire grâce à sa commande dump
(gdb) dump binary memory bytcodes_function 0x7ffff7cc5000 0x7ffff7cc5101
Je vous invite donc maintenant à installer miasm.
Résolution avec Miasm
Pour cette partie nous allons utiliser le framework miasm afin de résoudre ce code.
Voici mon code permettant de trouver les entrées correctes à notre fonction. J’ai commenté le code au maximum, néanmoins je vais quand même vous résumer son fonctionnement afin d’être sur que tout le monde comprenne.
Le programme va dans un premier temps lire les octets que l’on a dump précedemmemnt, les interpreter puis lancer une execution symbolique sur notre code. A la suite de cette exécution symbolique il va récuperer l’expression symbolique du registre RAX, qui est le registre qui contient notre valeur de retour et la transformer en contrainte compréhensible par z3. A partir de là on va simplifier cette expression et la résoudre.
from miasm.analysis.machine import Machine
from miasm.core.locationdb import LocationDB
from miasm.analysis.binary import Container
from miasm.expression.expression import *
from miasm.ir.symbexec import SymbolicExecutionEngine
from miasm.ir.translators.z3_ir import TranslatorZ3
from miasm.arch.x86.lifter_model_call import LifterModelCall_x86_64
from miasm.analysis.simplifier import *
from miasm.expression.simplifications import expr_simp, ExpressionSimplifier
from z3 import *
import re
def solve_shellcode(shellcode):
# on créé une nouvelle location pour notre shellcode
loc_db = LocationDB()
# on load notre shellcode (nos bytes code)
container = Container.from_string(shellcode, loc_db)
machine = Machine('x86_64')
ira = machine.lifter(loc_db)
dis_engine = machine.dis_engine(container.bin_stream, loc_db=loc_db)
start_addres = 0
# https://github.com/cea-sec/miasm/blob/master/doc/ir/lift.ipynb
asm_cfg = dis_engine.dis_multiblock(start_addres)
ira_cfg = ira.new_ircfg_from_asmcfg(asm_cfg)
"""
# on peut utiliser ce bout de code pour afficher les instructions assembleurs.
for block in asm_cfg.blocks:
print(block)
"""
init_state = {}
# on definit ici RDI qui va contenir la valeur en entrée.
init_state[ExprId("RDI", 64)] = ExprId('input', 64)
# rax qui est censé être égal à 0 à la fin du script.
init_state[ExprId("RAX", 64)] = ExprId('result', 64)
# on lance l'execution symbolique.
sb = SymbolicExecutionEngine(LifterModelCall_x86_64(loc_db) , state=init_state)
sb.run_at(ira_cfg, addr=start_addres)
# on va transformer l'expression symbolique en contraintes pour z3
trans = TranslatorZ3(loc_db=loc_db)
# solveur basique z3
s = Solver()
# on utilise miasm pour simplifier les expressions symboliques (on aurait pu faire sans pour ce chall)
expr_simp_cond = ExpressionSimplifier()
expr_simp_cond.enable_passes(ExpressionSimplifier.PASS_COND)
# récuperer l'expression symbolique (+ la simplifiée.)
expr_rax = sb.eval_expr(expr_simp(expr_simp_cond(ExprId('RAX', 64))))
# on solve avec z3
s.add(trans.from_expr(expr_rax) == trans.from_expr(ExprInt(0, 64)))
if s.check() == sat:
# print("found")
model = s.model()
# on retourne le resultat
# (j'ai honte de mon parsing mais je n'arrivais pas récuperer cette valeur correctement ...)
return int(re.findall("[0-9]+", str(model))[0])
else:
print("[-] fail")
return 0
# on ouvre le fichier contenant les octets de notre code assembleur
with open("bytcodes_function", "rb") as file:
content = file.read()
result =
solve_shellcode(content)
if result:
print(f"[+] solution found : {result}")
On va donc executer notre programme et l’on récupère bel et bien une valeur.
╭─user@arch-vmware ~/shared/fcsc2023/reverse/chaussette-xs
╰─➤ python3 solve_first_shellcode.py
[+] solution found : 14171339039947875846
On peut entrer ces valeurs dans notre binaire et effectivemment notre script passe la première condition avec succès !
Vous croyez que c’était fini ? c’est que le début.
On passe donc à la deuxième fonction. Comme précédemment, on place notre breakpoint avant l’appel à la fonction et on l’affiche.
(gdb) b*0x000055555555612c
Breakpoint 1 at 0x55555555612c
(gdb) run
Starting program: /home/user/shared/fcsc2023/reverse/chaussette-xs/chaussette-xs
[Thread debugging using libthread_db enabled]
Using host libthread_db library "/usr/lib/libthread_db.so.1".
14171339039947875846
123
Breakpoint 1, 0x000055555555612c in ?? ()
(gdb) x/i $rip
=> 0x55555555612c: call 0x555555557000
(gdb) x/110i 0x555555557000
0x555555557000: movabs rax,0x676e656c6c616863
0x55555555700a: push r15
0x55555555700c: push r14
0x55555555700e: push r13
0x555555557010: push r12
0x555555557012: push rbp
0x555555557013: push rbx
0x555555557014: mov rbx,rdi
0x555555557017: lea rdi,[rip+0xfea] # 0x555555558008
0x55555555701e: sub rsp,0x68
0x555555557022: movdqa xmm0,XMMWORD PTR [rip+0xfe6] # 0x555555558010
0x55555555702a: mov QWORD PTR [rsp+0x8],rsi
0x55555555702f: movups XMMWORD PTR [rsp+0x30],xmm0
0x555555557034: movdqa xmm0,XMMWORD PTR [rip+0xfe4] # 0x555555558020
0x55555555703c: mov QWORD PTR [rsp],rdx
0x555555557040: mov QWORD PTR [rsp+0x50],rax
0x555555557045: mov DWORD PTR [rsp+0x58],0x72662e65
0x55555555704d: mov BYTE PTR [rsp+0x5c],0x0
0x555555557052: movups XMMWORD PTR [rsp+0x40],xmm0
0x555555557057: call 0x5555555550a0 <getprotobyname@plt>
0x55555555705c: test rax,rax
0x55555555705f: je 0x5555555571bf
0x555555557065: mov edx,DWORD PTR [rax+0x10]
0x555555557068: mov esi,0x1
0x55555555706d: mov edi,0x2
0x555555557072: call 0x5555555550f0 <socket@plt>
0x555555557077: mov DWORD PTR [rip+0x313b],eax # 0x55555555a1b8
0x55555555707d: cmp eax,0xffffffff
0x555555557080: je 0x5555555571bf
0x555555557086: lea rdi,[rsp+0x30]
0x55555555708b: call 0x555555555090 <gethostbyname@plt>
0x555555557090: test rax,rax
0x555555557093: je 0x5555555571bf
0x555555557099: mov rax,QWORD PTR [rax+0x18]
0x55555555709d: mov rax,QWORD PTR [rax]
0x5555555570a0: mov edi,DWORD PTR [rax]
0x5555555570a2: call 0x555555555050 <inet_ntoa@plt>
0x5555555570a7: mov rdi,rax
0x5555555570aa: call 0x555555555080 <inet_addr@plt>
0x5555555570af: cmp eax,0xffffffff
0x5555555570b2: je 0x5555555571bf
0x5555555570b8: mov edi,DWORD PTR [rip+0x30fa] # 0x55555555a1b8
0x5555555570be: lea rsi,[rsp+0x20]
0x5555555570c3: mov DWORD PTR [rsp+0x24],eax
0x5555555570c7: mov edx,0x10
0x5555555570cc: mov DWORD PTR [rsp+0x20],0xcd080002
0x5555555570d4: call 0x5555555550e0 <connect@plt>
0x5555555570d9: cmp eax,0xffffffff
0x5555555570dc: je 0x5555555571bf
0x5555555570e2: lea r12,[rsp+0x18]
0x5555555570e7: lea r13,[rsp+0x10]
0x5555555570ec: lea r14,[rsp+0x8]
0x5555555570f1: nop DWORD PTR [rax+0x0]
0x5555555570f8: mov rax,QWORD PTR [rsp+0x8]
0x5555555570fd: mov edi,DWORD PTR [rip+0x30b5] # 0x55555555a1b8
0x555555557103: mov edx,0x8
0x555555557108: mov rsi,r12
0x55555555710b: mov QWORD PTR [rsp+0x18],rax
0x555555557110: call 0x555555555040 <write@plt>
0x555555557115: mov rax,QWORD PTR [rsp]
0x555555557119: mov edx,0x8
0x55555555711e: mov rsi,r12
0x555555557121: mov edi,DWORD PTR [rip+0x3091] # 0x55555555a1b8
0x555555557127: mov QWORD PTR [rsp+0x18],rax
0x55555555712c: call 0x555555555040 <write@plt>
0x555555557131: mov edi,DWORD PTR [rip+0x3081] # 0x55555555a1b8
0x555555557137: mov edx,0x8
0x55555555713c: mov rsi,r13
0x55555555713f: call 0x555555555070 <read@plt>
0x555555557144: mov rbp,QWORD PTR [rsp+0x10]
0x555555557149: cmp rbp,0xffffffffffffffff
0x55555555714d: je 0x5555555571ce
0x55555555714f: mov r15,rbx
0x555555557152: test rbp,rbp
0x555555557155: jne 0x55555555716e
0x555555557157: jmp 0x555555557189
0x555555557159: nop DWORD PTR [rax+0x0]
0x555555557160: add r15,rax
0x555555557163: mov rax,r15
0x555555557166: sub rax,rbx
0x555555557169: cmp rax,rbp
0x55555555716c: jae 0x555555557189
0x55555555716e: mov edi,DWORD PTR [rip+0x3044] # 0x55555555a1b8
0x555555557174: xor ecx,ecx
0x555555557176: mov edx,0x1000
0x55555555717b: mov rsi,r15
0x55555555717e: call 0x555555555030 <recv@plt>
0x555555557183: cmp rax,0xffffffffffffffff
0x555555557187: jne 0x555555557160
0x555555557189: mov rsi,r14
0x55555555718c: lea rdi,[rip+0xe71] # 0x555555558004
0x555555557193: xor eax,eax
0x555555557195: call 0x5555555550d0 <__isoc99_scanf@plt>
0x55555555719a: mov rsi,rsp
0x55555555719d: lea rdi,[rip+0xe60] # 0x555555558004
0x5555555571a4: xor eax,eax
0x5555555571a6: call 0x5555555550d0 <__isoc99_scanf@plt>
0x5555555571ab: mov rsi,QWORD PTR [rsp]
0x5555555571af: mov rdi,QWORD PTR [rsp+0x8]
0x5555555571b4: call rbx
0x5555555571b6: test rax,rax
0x5555555571b9: je 0x5555555570f8
0x5555555571bf: add rsp,0x68
0x5555555571c3: pop rbx
0x5555555571c4: pop rbp
0x5555555571c5: pop r12
0x5555555571c7: pop r13
0x5555555571c9: pop r14
0x5555555571cb: pop r15
0x5555555571cd: ret
cette fonction peut paraître effrayante aux premiers abords, mais elle est en réalité plutôt simple. On peut d’abord voir les appels aux fonctions de la libc tels que socket, connect, recv etc.
Elle va établir une connexion tcp avec un serveur distant, lui envoyer nos 2 valeurs entrées précédemment et récuperer des données que le serveur lui envoie. Les octets que la fonction récupère vont être placés à l’addresse de notre précédente fonction. Ensuite le programme va demander à nouveau 2 entrées à l’utilisateur et appeler notre nouvelle fonction avec les valeurs données par l’utlisateur et recommencer.
On pourrait représenter le fonctionnement de cette fonction par le pseudo code suivant :
void strange_function(char* shellcode, ulong value1, ulong value2)
{
conn = connexion(); // établit une connexion tcp avec le serveur
while (1)
{
size = read(conn, 8); // lit 8 octets qui seront la taille du shellcode
*shellcode = recv(conn) // reçois le shellcode et l'écris à
// l'addresse de l'ancien shellcode
// récupère les 2 entrées utilisateur
scanf("%lu", &value1);
scanf("%lu", &value2);
// verifie que les entrées résolve le shellcode.
// pareil que la première partie du challenge.
if ((*(void(*)())shellcode)(value1, value2) != 0)
{
// signifie que notre entrée est fausse
// le programme se stoppe. (et donc par conséquent pas de flag)
return;
}
}
}
On va donc récuperer l’IP et le port afin de créer nous même la connexion tcp avec le serveur distant, lui envoyer nos valeurs et récuperer les shellcodes.
Pour récuperer l’ip et le port on pourrait placer un point d’arret au niveau de l’appel à la fonction getprotobyname et au niveau de la fonction socket . Mais étant flemmard (ou malin à vous de me dire) j’ai préféré regarder les connexions ouvertes sur ma machine par le processus en question.

Pour ce faire j’ai utilisé l’outil ss. J’execute donc mon binaire, je lui donne les valeurs trouvé précedemment afin qu’il établisse la connexion et ensuite avec la commande ss -nap | grep chaussette-xs je récupère l’ip et le port.
Le serveur distant se trouve donc en 51.254.115.216:2253.
Résoudre les shellcode avec miasm
Après quelques tests on s’aperçoit qu’a chaque connexion le code renvoyé par le serveur change. On va donc implémenter un algorithme qui resout les fonctions donnée par le serveur distant.
Heureusement nous avons déjà fait une grande partie du travail, en effet nous avons implémenté durant la première partie une fonction qui utilise miasm afin de résoudre les shellcodes. Nous avons donc a configurer la connexion avec le serveur et ensuite résoudre les instructions que le serveur nous enverra.
Voici mon code :
from pwn import *
from miasm.analysis.machine import Machine
from miasm.core.locationdb import LocationDB
from miasm.analysis.binary import Container
from miasm.expression.expression import *
from miasm.ir.symbexec import SymbolicExecutionEngine
from miasm.ir.translators.z3_ir import TranslatorZ3
from miasm.arch.x86.lifter_model_call import LifterModelCall_x86_64
from miasm.analysis.simplifier import *
from miasm.expression.simplifications import expr_simp, ExpressionSimplifier
from z3 import *
import re
def solve_shellcode(shellcode):
# on créé une nouvelle location pour notre shellcode
loc_db = LocationDB()
# on load notre shellcode
container = Container.from_string(shellcode, loc_db)
machine = Machine('x86_64')
ira = machine.lifter(loc_db)
dis_engine = machine.dis_engine(container.bin_stream, loc_db=loc_db)
start_addres = 0
# https://github.com/cea-sec/miasm/blob/master/doc/ir/lift.ipynb
asm_cfg = dis_engine.dis_multiblock(start_addres)
ira_cfg = ira.new_ircfg_from_asmcfg(asm_cfg)
"""
# on peut utiliser ce bout de code pour afficher les instructions assembleurs.
for block in asm_cfg.blocks:
print(block)
"""
init_state = {}
# on definit ici RDI qui va contenir la valeur en entrée.
init_state[ExprId("RDI", 64)] = ExprId('input', 64)
# rax qui est censé être égal à 0 à la fin du script.
init_state[ExprId("RAX", 64)] = ExprId('result', 64)
# on lance l'execution symbolique.
sb = SymbolicExecutionEngine(LifterModelCall_x86_64(loc_db) , state=init_state)
sb.run_at(ira_cfg, addr=start_addres)
# on va transformer l'expression symbolique en contraintes pour z3
trans = TranslatorZ3(loc_db=loc_db)
# solveur basique z3
s = Solver()
# on utilise miasm pour simplifier les expressions symboliques (on aurait pu faire sans pour ce chall)
expr_simp_cond = ExpressionSimplifier()
expr_simp_cond.enable_passes(ExpressionSimplifier.PASS_COND)
# récuperer l'expression symbolique (+ la simplifiée.)
expr_rax = sb.eval_expr(expr_simp(expr_simp_cond(ExprId('RAX', 64))))
# on solve avec z3
s.add(trans.from_expr(expr_rax) == trans.from_expr(ExprInt(0, 64)))
if s.check() == sat:
# print("found")
model = s.model()
return int(re.findall("[0-9]+", str(model))[0])
else:
print("[-] fail")
print(shellcode)
return 0
# j'ai placé mon breakpoint au final, je trouvai un hostname plus joli
host = "challenges.france-cybersecurity-challenge.fr"
port = 2253
data_1 = 14171339039947875846
data_2 = 0xdeadbeef # useless
# on etablit la connection tcp.
p = remote(host, port)
compteur = 0
while 1:
# on envoie notre solution ainsi que celle inutile pour ce challenge.
p.send(data_1.to_bytes(8, "little"))
p.send(data_2.to_bytes(8, "little"))
size = int.from_bytes(p.recv(8), "little")
shellcode = b""
print(f"[~] shellcode of {size} bytes")
shellcode = p.recv(size)
flag = re.findall(b"FCSC{.*}", shellcode)
if flag:
print("flag is : ", end="")
print(flag[0].decode())
exit()
print(f"[~] solving shellcode {compteur}...")
result = solve_shellcode(shellcode)
if result:
data_1 = result
print(f"[+] solution found : {data_1}")
compteur += 1
else:
exit(1)
# on ferme la connection
p.close()
Ce code va établir une connexion avec le serveur et tant qu’il ne trouve pas le flag dans les fonctions qu’il reçoit il va les résoudre et renvoyer la solution. Je ne pense pas qu’il est nécessaire que j’explique mon script en détail, il est très similaire au précédent.
On execute donc le script et au bout de quelques secondes le flag apparait.
╭─user@arch-vmware ~/shared/fcsc2023/reverse/chaussette-xs
╰─➤ python3 solving_using_miasm.py
[+] Opening connection to challenges.france-cybersecurity-challenge.fr on port 2253: Done
[~] shellcode of 414 bytes
[~] solving shellcode 0...
[+] solution found : 16584048833465228239
[~] shellcode of 444 bytes
[~] solving shellcode 1...
[+] solution found : 5460636808995531285
[~] shellcode of 842 bytes
[~] solving shellcode 2...
[+] solution found : 3445377768356975671
[~] shellcode of 810 bytes
[~] solving shellcode 3...
[+] solution found : 6412023629681526002
[~] shellcode of 929 bytes
[~] solving shellcode 4...
[+] solution found : 1172201077721270149
[~] shellcode of 18446744073709551615 bytes
flag is : FCSC{2a86d6edc5d08afc03d2c9ef3e2ff83cd63e520ffbd716d96479df8147e6da5e}
[*] Closed connection to challenges.france-cybersecurity-challenge.fr port 2253
Pour conclure
J’ai trouvé ce challenge très intéressant, j’ai malheureusement été bloqué par son grand frère durant plusieurs jours sans le réussir. Il m’a néanmoins appris beaucoup de choses sur l’automatisation de l’analyse binaire. En effet j’ai toujours cru que les outils tels que angr, miasm et tout les solveurs de ce genre était pour les personnes qui ne voulaient pas réfléchir. C’était donc la première fois que j’utilisais miasm (et angr) et j’ai trouvé ça très intéressant. Cela m’a permis d’aborder un nouvel aspect du reverse engineering qui m’a l’air très complexe mais également très intéressant.