FCSC 2025 - Chatouille | TRIKKSS Blog

vous pouvez retrouver le binaire joint avec le chall ici

description du challenge

Découverte du challenge

Dans ce write-up, nous allons explorer un challenge de reverse engineering axé sur l’analyse d’un binaire utilisant des instructions AVX (Advanced Vector Extensions). J’ai passé (perdu ?) énormément de temps sur ce challenge en l’abordant de la mauvaise façon.

Analyse du binaire

La fonction principale est plutôt simple, celle-ci va lire une entrée utilisateur de 128 octets, verifier que la taille de celle-ci est de 118 octets et définir des valeurs aux indexs 0x76, 0x7E et 0x7F de notre buffer.

Ensuite elle va appeler 2 fonctions avec entrée notre binaire qui doivent chacune retourner 0.

int __fastcall main(int argc, const char **argv, const char **envp)
{
  int v3; // eax
  int v4; // edx
  int v5; // eax
  unsigned __int8 v7[128]; // [rsp+0h] [rbp-88h] BYREF

  memset(v7, 0, sizeof(v7));
  v3 = read(0, v7, 0x80uLL);
  if ( v3 <= 0 )
  {
    perror("read");
    exit(1);
  }
  v4 = v3;
  v5 = v3 - 1;
  if ( v7[v5] == 10 )
  {
    v7[v5] = 0;
    v4 = v5;
  }
  if ( v4 != 118
    || (v7[0x76] = 0x80, *(_WORD *)&v7[0x7E] = 0xB003, !shellcode_1((__int64)v7))
    || !shellcode_2((__int64)v7) )
  {
    puts(":(");
    exit(0);
  }
  puts("\\o/");
  return 0;
}

Analyse de la première fonction

Lorsque l’on ouvre la fonction, IDA ne parvient pas à produire une décompilation lisible pour cette fonction. La majorité du code est restituée en tant que séquence d’instructions assembleur brutes, sans traduction en C.

_BOOL8 __fastcall shellcode_1(__int64 _RDI)
{
  __asm
  {
    vmovdqa xmm7, cs:xmmword_7010
    vmovdqa xmm0, cs:xmmword_7120
    vmovdqa xmm13, cs:xmmword_7130
    vmovdqu xmm5, xmmword ptr [rdi]
    vmovdqa xmm12, cs:xmmword_7020
    vmovdqu xmm2, xmmword ptr [rdi+10h]
    vpalignr xmm14, xmm0, xmm13, 8
    vpshufb xmm15, xmm5, xmm7
    vmovdqu xmm6, xmmword ptr [rdi+20h]
    vpblendw xmm13, xmm13, xmm0, 0F0h
    vmovdqu xmm4, xmmword ptr [rdi+30h]
    vpaddd  xmm0, xmm15, xmm12
    vmovdqa xmm1, xmm13
    vmovdqa xmm3, xmm14
    vpshufb xmm6, xmm6, xmm7
    sha256rnds2 xmm1, xmm14, xmm0
    vmovdqa xmm11, cs:xmmword_7030
    vpshufb xmm2, xmm2, xmm7
    vpshufb xmm4, xmm4, xmm7
    vpshufd xmm0, xmm0, 0Eh
    vmovdqa xmm10, cs:xmmword_7040
    sha256msg1 xmm15, xmm2
    vpalignr xmm8, xmm4, xmm6, 4
    sha256rnds2 xmm3, xmm1, xmm0
    vpaddd  xmm0, xmm2, xmm11
    vmovdqa xmm9, cs:xmmword_7050
    sha256rnds2 xmm1, xmm3, xmm0
    vpaddd  xmm5, xmm15, xmm8
    vpshufd xmm0, xmm0, 0Eh
    sha256msg2 xmm5, xmm4
    sha256rnds2 xmm3, xmm1, xmm0
    vpaddd  xmm0, xmm6, xmm10
    vpalignr xmm15, xmm5, xmm4, 4
    sha256rnds2 xmm1, xmm3, xmm0
    sha256msg1 xmm2, xmm6
    vpshufd xmm0, xmm0, 0Eh
    vpaddd  xmm2, xmm2, xmm15
    sha256msg1 xmm6, xmm4
    sha256rnds2 xmm3, xmm1, xmm0

    [...]


    vpshufd xmm0, xmm0, 0Eh
    sha256msg2 xmm12, xmm13
    sha256rnds2 xmm4, xmm2, xmm0
    vpaddd  xmm0, xmm12, cs:xmmword_70B0
    vpalignr xmm9, xmm12, xmm13, 4
    sha256msg1 xmm13, xmm12
    vpaddd  xmm11, xmm11, xmm9
    sha256rnds2 xmm2, xmm4, xmm0
    vpshufd xmm0, xmm0, 0Eh
    sha256msg2 xmm11, xmm12
    sha256rnds2 xmm4, xmm2, xmm0
    vpaddd  xmm0, xmm11, cs:xmmword_70C0
    vpalignr xmm3, xmm11, xmm12, 4
    sha256msg1 xmm12, xmm11
    vpaddd  xmm10, xmm10, xmm3
    sha256rnds2 xmm2, xmm4, xmm0
    vpshufd xmm0, xmm0, 0Eh
    sha256msg2 xmm10, xmm11
    sha256rnds2 xmm4, xmm2, xmm0
    vpaddd  xmm0, xmm10, cs:xmmword_70D0
    vpalignr xmm9, xmm10, xmm11, 4
    sha256msg1 xmm11, xmm10
    vpaddd  xmm13, xmm13, xmm9
    sha256rnds2 xmm2, xmm4, xmm0
    vpshufd xmm0, xmm0, 0Eh
    sha256msg2 xmm13, xmm10
    sha256rnds2 xmm4, xmm2, xmm0
    vpaddd  xmm0, xmm13, xmm8
    vpalignr xmm8, xmm13, xmm10, 4
    sha256msg1 xmm10, xmm13
    vpaddd  xmm12, xmm12, xmm8
    sha256rnds2 xmm2, xmm4, xmm0
    vpshufd xmm0, xmm0, 0Eh
    sha256msg2 xmm12, xmm13
    sha256rnds2 xmm4, xmm2, xmm0
    vpaddd  xmm0, xmm12, xmm15
    vpalignr xmm15, xmm12, xmm13, 4
    vpaddd  xmm11, xmm11, xmm15
    sha256rnds2 xmm2, xmm4, xmm0
    vpshufd xmm0, xmm0, 0Eh
    sha256msg2 xmm11, xmm12
    sha256rnds2 xmm4, xmm2, xmm0
    vpaddd  xmm0, xmm11, xmm5
    vpalignr xmm5, xmm11, xmm12, 4
    vpaddd  xmm3, xmm10, xmm5
    sha256rnds2 xmm2, xmm4, xmm0
    vpshufd xmm0, xmm0, 0Eh
    sha256msg2 xmm3, xmm11
    sha256rnds2 xmm4, xmm2, xmm0
    vpaddd  xmm0, xmm3, xmm6
    sha256rnds2 xmm2, xmm4, xmm0
    vpshufd xmm0, xmm0, 0Eh
    sha256rnds2 xmm4, xmm2, xmm0
    vpaddd  xmm1, xmm2, xmm1
    vpaddd  xmm6, xmm4, xmm14
    vpshufd xmm2, xmm1, 0B1h
    vpshufd xmm14, xmm6, 1Bh
    vpblendw xmm4, xmm14, xmm2, 0F0h
    vpalignr xmm10, xmm2, xmm14, 8
    vpshufb xmm9, xmm4, xmm7
    vpxor   xmm13, xmm9, cs:xmmword_90C0
    vpshufb xmm7, xmm10, xmm7
    vptest  xmm13, xmm13
  }
  if ( !_ZF )
    return 0LL;
  __asm
  {
    vpxor   xmm8, xmm7, cs:xmmword_90D0
    vptest  xmm8, xmm8
  }
  return _ZF != 0;
}

Lorsque je tombe sur ce shellcode conséquent, j’ai une seule idée qui me vient tête : il va probablement falloir utiliser de l’execution symbolique pour résoudre le shellcode (spoil : non).

Je me lance alors durant plusieurs jours dans la résolution de cette unique fonction (il aurait peut être été plus intelligent de jeter un oeil à la deuxième fonction).

Le fait qu’IDA ne supporte pas cette instruction n’est pas une exception : je n’ai trouvé aucun outil d’exécution symbolique capable de l’interpréter. Je commence donc à essayer de résoudre le challenge avec Miasm, puis avec angr, puis avec Triton, puis en réimplémentant les instructions sha256 en C et recréant un binaire sur lequel j’allais pouvoir faire de l’execution symbolique avec angr … allant jusqu’a réimplémenter mon propre moteur d’exec symbolique avec capstone et z3 ! Tout ça en vain.

Après avoir passé beaucoup de temps sur la première fonction sans succès, j’ai décidé de m’attaquer à la seconde. Ce n’est qu’après un long moment, en lisant la documentation Intel sur les instructions sha, que j’ai remarqué que le code fourni en exemple, implémentant SHA-256 avec des instructions AVX, ressemblait fortement à celui de ma première fonction. En réalité, celle-ci ne faisait qu’un simple SHA-256 de l’input avant de le comparer à un hash stocké en mémoire ! Beaucoup de temps perdu (et de cheveux), certes, mais cela m’aura permis d’apprendre énormément de choses sur l’exécution symbolique.

De toute façon, si j’avais réussi à inverser un SHA-256 avec Z3, je serais probablement en train de négocier un poste à la NSA à l’heure qu’il est.

Analyse de la seconde fonction

Nous allons maintenant nous intéresser à la fonction clé du challenge.

Celle-ci est presque entièrement constitué de 2 opérations :

vpshufd
sha256msg1

Basiquement, cette fonction ressemble à ça. Je ne vous ai pas mis l’intégralité du code mais celui-ci est très très long et répétitif.

vmovdqu xmm6, xmmword ptr [rdi]
vmovdqu xmm0, xmmword ptr [rdi+10h]
vmovdqu xmm10, xmmword ptr [rdi+20h]
vpshufd xmm1, xmm6, 39h ; '9'
sha256msg1 xmm0, xmm6
vpshufd xmm2, xmm1, 39h ; '9'
sha256msg1 xmm0, xmm1
vpshufd xmm3, xmm2, 39h ; '9'
sha256msg1 xmm0, xmm2
vmovdqu xmm2, xmmword ptr [rdi+30h]
vpshufd xmm4, xmm3, 39h ; '9'
sha256msg1 xmm0, xmm3
vpshufd xmm5, xmm4, 39h ; '9'
sha256msg1 xmm0, xmm4
vpshufd xmm7, xmm5, 39h ; '9'
sha256msg1 xmm0, xmm5
vpshufd xmm8, xmm7, 39h ; '9'
sha256msg1 xmm0, xmm7
sha256msg1 xmm0, xmm8
vpshufd xmm9, xmm8, 39h ; '9'
vpshufd xmm11, xmm0, 39h ; '9'
sha256msg1 xmm10, xmm0
vpshufd xmm12, xmm11, 39h ; '9'
sha256msg1 xmm10, xmm11
vpshufd xmm13, xmm12, 39h ; '9'
sha256msg1 xmm10, xmm12
vpshufd xmm14, xmm13, 39h ; '9'
sha256msg1 xmm10, xmm13
vmovdqu xmm13, xmmword ptr [rdi+40h]
vpshufd xmm15, xmm14, 39h ; '9'
sha256msg1 xmm10, xmm14
vpshufd xmm6, xmm15, 39h ; '9'
sha256msg1 xmm10, xmm15
vpshufd xmm0, xmm6, 39h ; '9'
sha256msg1 xmm10, xmm6
sha256msg1 xmm10, xmm0
vpshufd xmm8, xmm0, 39h ; '9'
vpshufd xmm1, xmm10, 39h ; '9'
sha256msg1 xmm2, xmm10
vpshufd xmm3, xmm1, 39h ; '9'
sha256msg1 xmm2, xmm1
vpshufd xmm4, xmm3, 39h ; '9'
sha256msg1 xmm2, xmm3
vpshufd xmm5, xmm4, 39h ; '9'
sha256msg1 xmm2, xmm4
vpshufd xmm7, xmm5, 39h ; '9'
sha256msg1 xmm2, xmm5
vpshufd xmm10, xmm7, 39h ; '9'
sha256msg1 xmm2, xmm7
vmovdqu xmm7, xmmword ptr [rdi+50h]
vpshufd xmm11, xmm10, 39h ; '9'
sha256msg1 xmm2, xmm10
sha256msg1 xmm2, xmm11
vpshufd xmm12, xmm11, 39h ; '9'
vpshufd xmm14, xmm2, 39h ; '9'
sha256msg1 xmm13, xmm2
vpshufd xmm15, xmm14, 39h ; '9'
sha256msg1 xmm13, xmm14
vpshufd xmm6, xmm15, 39h ; '9'
sha256msg1 xmm13, xmm15
vpshufd xmm0, xmm6, 39h ; '9'
sha256msg1 xmm13, xmm6
vpshufd xmm2, xmm0, 39h ; '9'
sha256msg1 xmm13, xmm0
vmovdqu xmm0, xmmword ptr [rdi+60h]
vpshufd xmm1, xmm2, 39h ; '9'
sha256msg1 xmm13, xmm2
vpshufd xmm3, xmm1, 39h ; '9'
sha256msg1 xmm13, xmm1
sha256msg1 xmm13, xmm3
vpshufd xmm10, xmm3, 39h ; '9'
vpshufd xmm4, xmm13, 39h ; '9'
sha256msg1 xmm7, xmm13
vpshufd xmm5, xmm4, 39h ; '9'
sha256msg1 xmm7, xmm4
vpshufd xmm11, xmm5, 39h ; '9'
sha256msg1 xmm7, xmm5
vpshufd xmm13, xmm11, 39h ; '9'
sha256msg1 xmm7, xmm11
vpshufd xmm14, xmm13, 39h ; '9'
sha256msg1 xmm7, xmm13
vpshufd xmm15, xmm14, 39h ; '9'
sha256msg1 xmm7, xmm14
vpshufd xmm6, xmm15, 39h ; '9'
sha256msg1 xmm7, xmm15
vmovdqu xmm15, xmmword ptr [rdi+70h]
sha256msg1 xmm7, xmm6
vpshufd xmm5, xmm6, 39h ; '9'
vpshufd xmm2, xmm7, 39h ; '9'
sha256msg1 xmm0, xmm7
vpshufd xmm1, xmm2, 39h ; '9'
sha256msg1 xmm0, xmm2
vpshufd xmm3, xmm1, 39h ; '9'
sha256msg1 xmm0, xmm1
vpshufd xmm7, xmm3, 39h ; '9'
sha256msg1 xmm0, xmm3
vpshufd xmm4, xmm7, 39h ; '9'
sha256msg1 xmm0, xmm7
vpshufd xmm11, xmm4, 39h ; '9'
sha256msg1 xmm0, xmm4
vpshufd xmm13, xmm11, 39h ; '9'
sha256msg1 xmm0, xmm11
sha256msg1 xmm0, xmm13
vpshufd xmm14, xmm13, 39h ; '9'
vpshufd xmm6, xmm0, 39h ; '9'
sha256msg1 xmm15, xmm0
sha256msg1 xmm15, xmm6
vpshufd xmm0, xmm6, 39h ; '9'
vpshufd xmm2, xmm0, 39h ; '9'
sha256msg1 xmm15, xmm0
vpshufd xmm1, xmm2, 39h ; '9'
sha256msg1 xmm15, xmm2
vpshufd xmm3, xmm1, 39h ; '9'
sha256msg1 xmm15, xmm1
vpshufd xmm7, xmm3, 39h ; '9'
sha256msg1 xmm15, xmm3

[...] # 3875 lignes de vpshufd et sha256msg1

vpshufd xmm9, xmm2, 39h ; '9'
vpxor   xmm9, xmm9, cs:xmmword_9040
sha256msg1 xmm12, xmm8
vpshufd xmm8, xmm8, 39h ; '9'
vpshufd xmm1, xmm8, 39h ; '9'
sha256msg1 xmm12, xmm8
vpshufd xmm3, xmm1, 39h ; '9'
sha256msg1 xmm12, xmm1
vpshufd xmm4, xmm3, 39h ; '9'
sha256msg1 xmm12, xmm3
vpshufd xmm10, xmm4, 39h ; '9'
sha256msg1 xmm12, xmm4
vpshufd xmm6, xmm10, 39h ; '9'
sha256msg1 xmm12, xmm10
vpshufd xmm15, xmm6, 39h ; '9'
sha256msg1 xmm12, xmm6
sha256msg1 xmm12, xmm15
vpshufd xmm0, xmm15, 39h ; '9'
vpxor   xmm0, xmm0, cs:xmmword_9050
sha256msg1 xmm13, xmm12
vpshufd xmm12, xmm12, 39h ; '9'
vpshufd xmm2, xmm12, 39h ; '9'
sha256msg1 xmm13, xmm12
vpshufd xmm8, xmm2, 39h ; '9'
sha256msg1 xmm13, xmm2
vpshufd xmm1, xmm8, 39h ; '9'
sha256msg1 xmm13, xmm8
vpshufd xmm3, xmm1, 39h ; '9'
sha256msg1 xmm13, xmm1
vpshufd xmm4, xmm3, 39h ; '9'
sha256msg1 xmm13, xmm3
vpshufd xmm10, xmm4, 39h ; '9'
sha256msg1 xmm13, xmm4
sha256msg1 xmm13, xmm10
vpshufd xmm15, xmm10, 39h ; '9'
vpxor   xmm15, xmm15, cs:xmmword_9060
sha256msg1 xmm5, xmm13
vpshufd xmm13, xmm13, 39h ; '9'
vpshufd xmm6, xmm13, 39h ; '9'
sha256msg1 xmm5, xmm13
vpshufd xmm12, xmm6, 39h ; '9'
sha256msg1 xmm5, xmm6
vpshufd xmm2, xmm12, 39h ; '9'
sha256msg1 xmm5, xmm12
vpshufd xmm8, xmm2, 39h ; '9'
sha256msg1 xmm5, xmm2
vpshufd xmm1, xmm8, 39h ; '9'
sha256msg1 xmm5, xmm8
vpshufd xmm3, xmm1, 39h ; '9'
sha256msg1 xmm5, xmm1
sha256msg1 xmm5, xmm3
vpshufd xmm10, xmm3, 39h ; '9'
vpxor   xmm10, xmm10, cs:xmmword_9070
sha256msg1 xmm14, xmm5
vpshufd xmm5, xmm5, 39h ; '9'
vpshufd xmm4, xmm5, 39h ; '9'
sha256msg1 xmm14, xmm5
vpshufd xmm13, xmm4, 39h ; '9'
sha256msg1 xmm14, xmm4
vpshufd xmm6, xmm13, 39h ; '9'
sha256msg1 xmm14, xmm13
vpshufd xmm12, xmm6, 39h ; '9'
sha256msg1 xmm14, xmm6
vpshufd xmm2, xmm12, 39h ; '9'
sha256msg1 xmm14, xmm12
vpshufd xmm8, xmm2, 39h ; '9'
sha256msg1 xmm14, xmm2
sha256msg1 xmm14, xmm8
vpshufd xmm1, xmm8, 39h ; '9'
vpxor   xmm1, xmm1, cs:xmmword_9080
sha256msg1 xmm11, xmm14
vpshufd xmm14, xmm14, 39h ; '9'
vpshufd xmm3, xmm14, 39h ; '9'
sha256msg1 xmm11, xmm14
vpshufd xmm5, xmm3, 39h ; '9'
sha256msg1 xmm11, xmm3
vpshufd xmm4, xmm5, 39h ; '9'
sha256msg1 xmm11, xmm5
vpshufd xmm13, xmm4, 39h ; '9'
sha256msg1 xmm11, xmm4
vpshufd xmm6, xmm13, 39h ; '9'
sha256msg1 xmm11, xmm13
vpshufd xmm12, xmm6, 39h ; '9'
sha256msg1 xmm11, xmm6
vpor    xmm6, xmm0, xmm9
sha256msg1 xmm11, xmm12
vpshufd xmm2, xmm12, 39h ; '9'
vpxor   xmm2, xmm2, cs:xmmword_9090
sha256msg1 xmm7, xmm11
vpshufd xmm11, xmm11, 39h ; '9'
vpshufd xmm8, xmm11, 39h ; '9'
sha256msg1 xmm7, xmm11
vpor    xmm11, xmm6, xmm1
vpshufd xmm14, xmm8, 39h ; '9'
sha256msg1 xmm7, xmm8
vpshufd xmm3, xmm14, 39h ; '9'
sha256msg1 xmm7, xmm14
vpshufd xmm5, xmm3, 39h ; '9'
sha256msg1 xmm7, xmm3
vpor    xmm3, xmm15, xmm10
vpshufd xmm4, xmm5, 39h ; '9'
sha256msg1 xmm7, xmm5
vpor    xmm5, xmm3, xmm2
vpshufd xmm13, xmm4, 39h ; '9'
sha256msg1 xmm7, xmm4
vpshufd xmm12, xmm13, 39h ; '9'
sha256msg1 xmm7, xmm13
vpxor   xmm8, xmm12, cs:xmmword_90A0
vpxor   xmm7, xmm7, cs:xmmword_90B0
vpxor   xmm12, xmm12, xmm12
vpor    xmm14, xmm11, xmm8
vpor    xmm4, xmm5, xmm7
vpor    xmm13, xmm14, xmm4
vpcmpeqd xmm0, xmm13, xmm12
vpmovmskb eax, xmm0
cmp     eax, 0FFFFh
setz    dl
movzx   eax, dl
retn

L’instruction vpshufd

L’instruction vpshufd (Vector Packed Shuffle Doublewords) sert à réorganiser les éléments d’un vecteur de 128 ou 256 bits. Chaque élément du vecteur est un entier de 32 bits (appelé “doubleword”). L’opération utilise un masque de contrôle pour déterminer comment les éléments doivent être mélangés : pour chaque position dans le résultat, le masque indique quel élément source doit être copié.

Concrètement, vpshufd est utilisée pour :
Permuter les éléments d’un vecteur selon un ordre précis,
Dupliquer certains éléments si nécessaire,
Réorganiser les données pour des calculs parallèles plus efficaces.

Elle est très utilisée dans le traitement de données vectorielles, la cryptographie, et l’optimisation des algorithmes SIMD.

Source: ChatGPT

Dans notre cas l’instruction est toujours appelé avec l’argument 0x39, on peut donc la traduire par simple rotation de 32 bits vers la droite sur le registre en entrée.

De plus, il est intéressant de noter que toutes les 4 appels à vpshufd, la valeur retrouve son état initial.

L’instruction sha256msg1

D’après la document de intel, sha256msg1 (ainsi que sa soeur sha256msg2) semble servir à aider à faciliter génération du message schedule dans SHA-256. sert à faciliter la génération du message schedule dans SHA-256. Ne connaissant pas en détail le fonctionnement interne de SHA-256, cela reste un peu flou pour moi. Toutefois, pour ce challenge, il suffit de comprendre comment fonctionne cette instruction et non pas les autres.

Voici un schéma du fonctionnement de celle-ci :

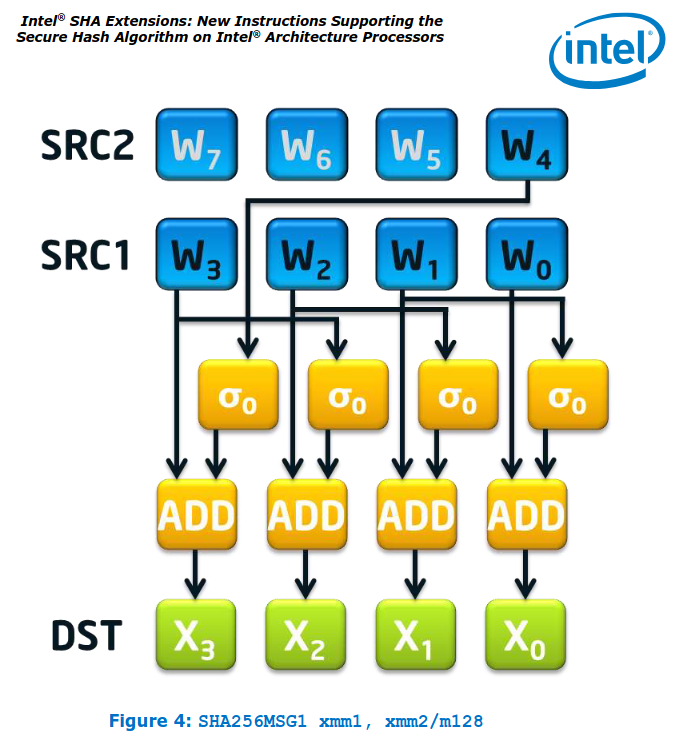
sha256msg1

On peut très facilement la réimplémenter de la manière suivante :

#include <stdio.h>
#include <stdint.h>
#include <string.h>
#include <x86intrin.h>

#define ROTR(x,y) (((x & 0xffffffff) >> (y & 31)) | (x << (32 - (y & 31)))) & 0xffffffff
#define SHR(x,n)  ((x) >> (n))

static inline uint32_t sigma0(uint32_t x) {
    return ROTR(x, 7) ^ ROTR(x, 18) ^ SHR(x, 3);
}

__m128i sha256msg1_manual(__m128i a, __m128i b) {
    uint32_t x[4], y[4];

    _mm_storeu_si128((__m128i*)x, a); // split la valeur sur 128 bits en blocs de 32 bits.
    _mm_storeu_si128((__m128i*)y, b);

    uint32_t r[4];
    r[0] = sigma0(x[1]) + x[0];
    r[1] = sigma0(x[2]) + x[1];
    r[2] = sigma0(x[3]) + x[2];
    r[3] = sigma0(y[0]) + x[3];

    return _mm_set_epi32(r[3], r[2], r[1], r[0]);
}

void print_xmm(__m128i v, const char* label) {
    uint8_t bytes[16];
    _mm_storeu_si128((__m128i*)bytes, v);
    printf("%s: 0x", label);
    for (int i = 15; i >= 0; i--) {
        printf("%02X", bytes[i]);
    }
    printf("\n");
}

int main() {
    /*
    on vient tester que notre implémentation retourne bien les mêmes résultats
    que l'instruction AVX
    */
    __m128i xmm0;
    __m128i xmm6;

    xmm0 = _mm_set_epi32(0x45454545, 0x44444444, 0x42424242, 0x41414141);
    xmm6 = _mm_set_epi32(0x38373635, 0x34333231, 0x48474645, 0x44434241);
    xmm0 = sha256msg1_manual(xmm0, xmm6); // implém custom
    print_xmm(xmm0, "sha256msg1 made home");

    xmm0 = _mm_set_epi32(0x45454545, 0x44444444, 0x42424242, 0x41414141);
    xmm6 = _mm_set_epi32(0x38373635, 0x34333231, 0x48474645, 0x44434241);
    xmm0 = _mm_sha256msg1_epu32(xmm0, xmm6); // instruction AVX
    print_xmm(xmm0, "sha256msg1 official");

    return 0;
}

En compilant et exécutant le code de test, on peut vérifier que notre implémentation de sha256msg1 est correcte :

╭─trikkss@arch-linux ~/ctf/FCSC-2025/reverse/chatouille/tests
╰─➤  gcc -mavx -msha test.c -o test
╭─trikkss@arch-linux ~/ctf/FCSC-2025/reverse/chatouille/tests
╰─➤  ./test
sha256msg1 made home: 0x9FD6052117B7B7B7D35353535D9D9D9D
sha256msg1 official: 0x9FD6052117B7B7B7D35353535D9D9D9D

Compréhension de l’algorithme

Il faut maintenant comprendre comment sont utilisées ces deux instructions.

Heureusement, après un long moment à contempler cette fonction les yeux dans le vide, j’ai fini par repérer un pattern. En effet, la fonction peut être divisé en bloc de 8 appels à vpshufd et 8 appels à sha256msg1.

Si l’on prend ce premier bloc, on se rend compte que celui-ci prend 2 bloc de 128 bits de notre entrée utilisateur et va ensuite appliquer 8 vpshufd puis effectuer 8 sha256msg1 avec chacun des outputs du vpshufd.

Voici une partie simplifiée et commenté d’un bloc du shellcode.

// récupère d2 blocs de 16 octets
vmovdqu xmm6, xmmword ptr [rdi]
vmovdqu xmm0, xmmword ptr [rdi+10h]

// applique les transformations sur RDI
vpshufd xmm1, xmm6, 39h
vpshufd xmm2, xmm1, 39h
vpshufd xmm3, xmm2, 39h
vpshufd xmm4, xmm3, 39h
vpshufd xmm5, xmm4, 39h
vpshufd xmm7, xmm5, 39h
vpshufd xmm8, xmm7, 39h
vpshufd xmm9, xmm8, 39h

// effectue 8 sha256msg1 sur xmm0 avec les transfo précédentes
sha256msg1 xmm0, xmm6
sha256msg1 xmm0, xmm1
sha256msg1 xmm0, xmm2
sha256msg1 xmm0, xmm3
sha256msg1 xmm0, xmm4
sha256msg1 xmm0, xmm5
sha256msg1 xmm0, xmm7
sha256msg1 xmm0, xmm8

Ce bloc est ensuite réapliqué pour chaque bloc de 16 octets de notre entré utilisateur avec cette fois le résultat du bloc précédent comme deuxième opérande pour sha256msg1.

Voici un schéma illustrant les 8 premiers blocs :

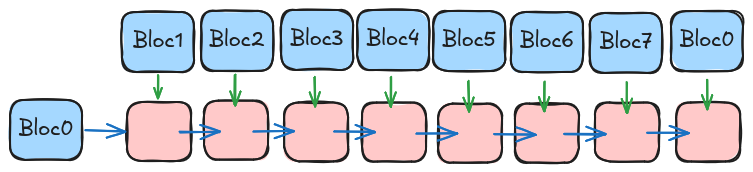
schéma premiers blocs

La sortie de chaque bloc (en rose) sert comme entrée à au prochain bloc.

Mais une fois que l’on a itéré sur toute notre entrée utilisateur, comment cela se passe-t-il ensuite ?

Et bien c’est tout simple (j’ai mis au moins 2h à comprendre), le prochain bloc prend en deuxième entrée le résultat du bloc n-8.

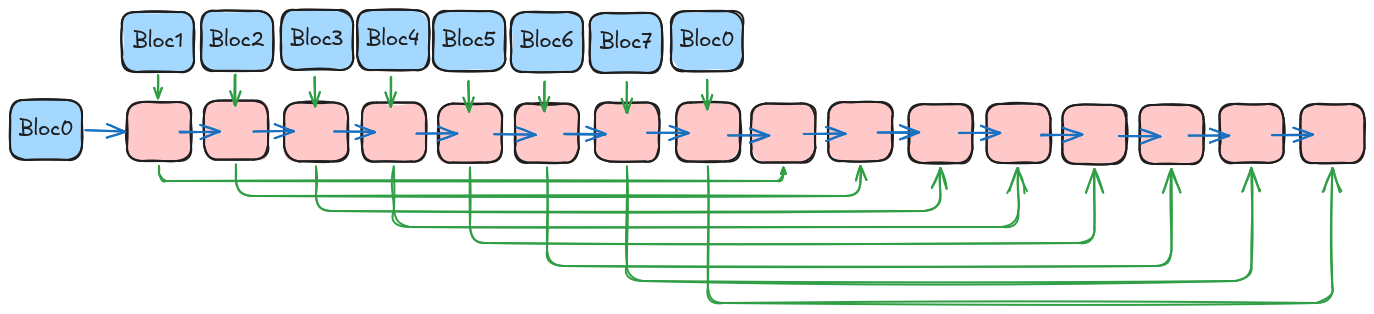
schéma sur plusieurs blocs

Et l’on va appliqué la même opération beaucoup de fois sur nos blocs jusqu’a la fin du shellcode.

Arrivé à la fin du shellcode, la sortie des 8 derniers blocs va être xoré avec des valeurs sur 128 bits. Afin que le shellcode retourne 0, il faut que les 8 derniers blocs soient égaux aux 8 valeurs par lesquelles ils sont xoré.

known_values = [
    0x27E2993E7DDB9BCE388260CED6DF027E, # dernier bloc
    0xAB509EB2143D13035F595D84BF7A1DBF, # avant dernier
    0x67172D37B77DAEFE99DB1D1FF04FBED5, # avant avant dernier
    0x4325F6DFDC17B3D93A437A2FD174192F, # etc.
    0xB6CEB5305C48B5C137C1EEC542DD7AB5,
    0x36DE1DABA4D0C410A59ABC08D9270088,
    0x4FB98600728660ADC7EB49ABF5F4BB97,
    0xBD7A8C92FE4A7BD964145C1B415E27FE
]

Voici une illustration du dernier bloc, en jaune nous pouvons retrouver les valeurs connues (et en bleu les inconnues, si jamais le point d’interrogation n’était pas assez explicite).

last blocks

On peut donc supposer que pour résoudre ce challenge il va falloir partir des 8 dernières valeurs connues et remonter les blocs jusqu’a arriver au premier.

Pour se faire, j’ai implémenter nos blocs en python afin de les résoudres à l’aide de z3.

Résolution avec z3

Voici mon implémentation d’un bloc avec z3 en python :

from z3 import *

def S0(x):
    return RotateRight(x,7) ^ RotateRight(x,18) ^ LShR(x,3)

def sha256msg1(src1, src2):
    X = [
        Extract(31,  0,  src1),
        Extract(63, 32,  src1),
        Extract(95, 64,  src1),
        Extract(127,96,  src1),
    ]
    Y = [
        Extract(31,  0,  src2),
        Extract(63, 32,  src2),
        Extract(95, 64,  src2),
        Extract(127,96,  src2),
    ]

    mask32 = BitVecVal(0xFFFFFFFF, 32)
    R0 = (S0(X[1]) + X[0]) & mask32
    R1 = (S0(X[2]) + X[1]) & mask32
    R2 = (S0(X[3]) + X[2]) & mask32
    R3 = (S0(Y[0]) + X[3]) & mask32

    return Concat(R3, R2, R1, R0)

def block(src1, src2):
    out = src1
    for i in range(8):
        out = sha256msg1(out, RotateRight(src2, 32*i))
    return out

On peut ainsi retrouver notre première inconue en partant de la fin en appelant le code suivant :

s = Solver()

s.add(block(BitVec('x', 128), BitVecVal(0xAB509EB2143D13035F595D84BF7A1DBF, 128)) ==  BitVecVal(0x27E2993E7DDB9BCE388260CED6DF027E, 128))

if s.check() == sat:
  print(s.model())
else:
  print("no solution found ...")

Maintenant il nous reste plus qu’a remonter les blocs jusqu’a trouver notre valeur initiale !

Pour ça on va compter le nombre de fois qu’apparait l’instruction sha256msg1 dans le shellcode.

╭─trikkss@arch-linux ~/ctf/FCSC-2025/reverse/chatouille
╰─➤  cat shellcode2.txt | grep sha256msg1 | wc -l
2040

Sachant que chaque bloc utilise 8 fois l’instruction on peut donc diviser par 8 ce qui nous donne 255 blocs à remonter.

Voici donc le script final :

from z3 import *

def S0(x):
    return RotateRight(x,7) ^ RotateRight(x,18) ^ LShR(x,3)

def sha256msg1(src1, src2):
    X = [
        Extract(31,  0,  src1),  # X[0]
        Extract(63, 32,  src1),  # X[1]
        Extract(95, 64,  src1),  # X[2]
        Extract(127,96,  src1),  # X[3]
    ]
    Y = [
        Extract(31,  0,  src2),  # Y[0]
        Extract(63, 32,  src2),  # Y[1]
        Extract(95, 64,  src2),  # Y[2]
        Extract(127,96,  src2),  # Y[3]
    ]

    mask32 = BitVecVal(0xFFFFFFFF, 32)
    R0 = (S0(X[1]) + X[0]) & mask32
    R1 = (S0(X[2]) + X[1]) & mask32
    R2 = (S0(X[3]) + X[2]) & mask32
    R3 = (S0(Y[0]) + X[3]) & mask32

    return Concat(R3, R2, R1, R0)

def block(src1, src2):
    out = src1
    for i in range(8):
        out = sha256msg1(out, RotateRight(src2, 32*i))
    return out

round_values = [
    0x27E2993E7DDB9BCE388260CED6DF027E,
    0xAB509EB2143D13035F595D84BF7A1DBF,
    0x67172D37B77DAEFE99DB1D1FF04FBED5,
    0x4325F6DFDC17B3D93A437A2FD174192F,
    0xB6CEB5305C48B5C137C1EEC542DD7AB5,
    0x36DE1DABA4D0C410A59ABC08D9270088,
    0x4FB98600728660ADC7EB49ABF5F4BB97,
    0xBD7A8C92FE4A7BD964145C1B415E27FE,
]

for i in range(255):
    s = Solver()

    x = BitVec('x', 128)
    y = BitVecVal(round_values[(i + 1) % len(round_values)], 128)

    s.add(block(x, y) == BitVecVal(round_values[i % len(round_values)], 128))

    if s.check() == sat:
        m = s.model()
        round_values[i % len(round_values)] = m[x].as_long()
    else:
        print("no solution found ...")
        exit()

print(b''.join(x.to_bytes(16, "little") for x in round_values[::-1]))

et on obtiens notre flag en sortie !

╭─trikkss@arch-linux ~/ctf/FCSC-2025/reverse/chatouille
╰─➤  python3 final-solve.py
b'FCSC{Shoh4IeFohmee1oichoo5iujohze2riPuuroochoh3vi0aGai5ae5aithooph2wohquai2takaeng9eeF3ue8QuooT2shiege5ee5ahL1vanoAnZ}\x80\x00\x00\x00\x00\x00\x00\x00\x03\xb0'

Découverte du challenge#

Analyse du binaire#

Analyse de la première fonction#

Analyse de la seconde fonction#

L’instruction vpshufd#

L’instruction sha256msg1#

Compréhension de l’algorithme#

Résolution avec z3#